How to deal with masts, their stays and their fittings? I could just do a piece by piece description of the various fittings, but I think that in doing so you would miss the broader picture which does much to explain why masts and their associated pieces are as they are. So I’m going to follow the logic(?) established earlier by first addressing the engineering aspects of masts and stays. I should at this stage warn you that it is going to take a number of articles to do this, and it may initially seem to consist of digressions followed by sub-digressions before we tackle the more practical aspects. I hope you will bear with me.
Of trees and simple masts.
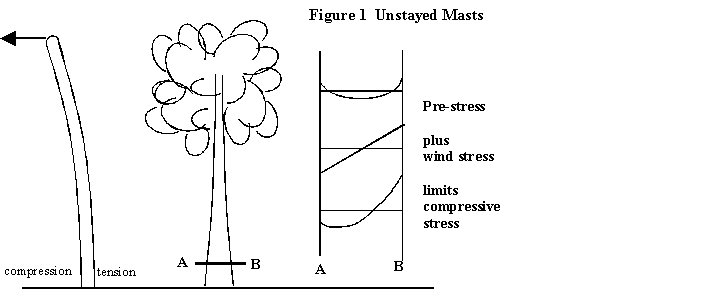
The conceptually simplest way to rig a mast – and almost certainly the earliest historically – is to plonk a self-supporting mast into the hull. Let’s say we have a 6m long stick in a hull whose beam is 2m. Let’s further assume that the principal loading from the sail is 500kg at the masthead, which is the kind of loading one would get from a squaresail or a lugsail. In the absence of any stays, the mast is going to bend. The maximum bending moment, and hence stress is at deck level – see Figure 1.
Wood is less strong in compression than tension, so what will happen when it breaks is that the fibres will progressively rupture on the compressive side of the mast until the whole thing falls over, perhaps breaking the outermost fibres on the tensile side as it goes. Using data for Douglas Fir, the diameter of stick needed in this instance would be about 280mm (about 11” in old money). The relationship between the diameter at the deck and the maximum loading is to the power of three, so if you were to double the diameter, the mast could withstand eight times the load at the masthead. Conversely the maximum loading for a given diameter varies in direct proportion with the maximum permissible stress. Douglas Fir can take about 15 Newtons per square millimetre (N/mm2), modern fibres about 400 N/mm2. So a carbon fibre mast to do the same job could be about 95mm diameter. Hence the increased use of unstayed masts in modern materials in craft such as Roxanne.
Now the more thoughtful amongst you may be wondering why trees – which are effectively unstayed masts – don’t blow over more often. There are two main reasons. Firstly and most obviously, they tend to be constructed in such a way that the trunks are thicker at the ground than they are further up, so they put more material where it is needed. But they are also constructed in such a way as to mitigate the relative weakness of wood in compression. How it is done is that the sap wood is pre-tensioned against the heart of the tree, so that the outer parts are all in tension. Add the stresses of the wind blowing on the tree, and that reduces the compressive stress on the downwind side, which is useful, at the cost of increasing the tensile stresses on the upwind side, which doesn’t matter. Clever stuff, and incidentally exactly the opposite of pre-stressed concrete, where the tension in the reinforcing rods induces compression in the surrounding concrete, which mitigates the fact that concrete is very weak in tension. Now just in case you thought that this was a sub-digression, there is a practical application for those of you who wish to fashion a mast from a tree trunk. To get the strongest mast, keep as much of the original wood as possible to retain the built-in pre-stresses.
Staying Power
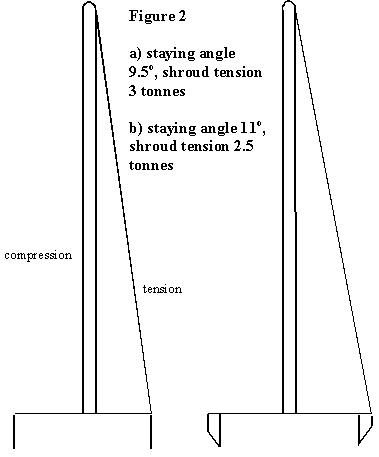
Adding a stay to our mast changes the picture completely, whether it is a permanent stay or a halyard set to windward as in dipping luggers or Viking longboats. What happens – see Figure 2 – is that the bending is more or less eradicated by building up tensile loads in the stay. However, to stop the mast disappearing down through the keel, a corresponding compression is induced in the mast. For our 6m mast with 500kg at the masthead, we are looking at about 3 tonnes tension in the stay, and about 3 tonnes (or 30,000 N) compression in the mast. Now if Douglas fir can stand a compressive stress of 15 N/mm2, all we need is 2000 square millimetres of mast section and we are there. That gives us a diameter of 50mm, as opposed to 280 mm. Hardly surprising that stayed masts are so widely used.
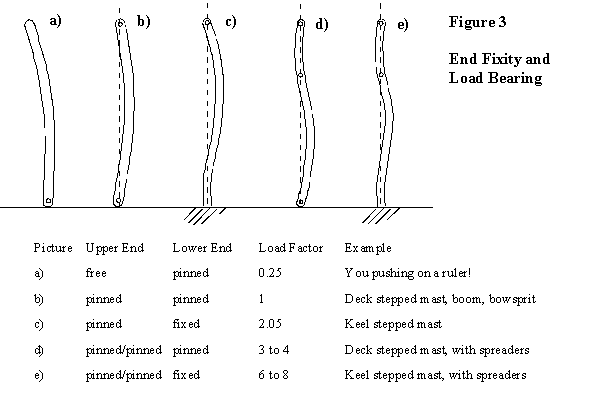
Ah, but hang on a moment while I lead you down the next digression. This one is to do with modes of compressive failure. Go and find something that is long and thin, a ruler perhaps or a thin stick. Now put one end on the floor or similar fixed point, and lean on the other, applying force along its length. You will find that the thing will bow out sideways at a fairly low load. Remove the load and it will spring back into its original shape none the worse for wear. This phenomenon is referred to as “elastic instability” or more commonly “buckling”. It differs fundamentally from failure modes like compressive rupture because it is principally dependent not on the strength of the material being loaded, but on other factors. Most important is the length of the item. The critical load varies inversely with the square of the length, so halving the length quadruples the maximum load. The next issue is what is referred to as the “fixity” of the ends. You have a choice of fixed – as in a keel stepped mast which is also held at deck level -, pinned, which is an end free to rotate but held in position, as in a deck stepped mast or the point at which a mast is stayed, or free, which is free to rotate and move, as in the end of an unstayed mast. Your ruler experiment would have had a free upper end and a pinned lower end. I hope Figure 3 (below) makes this clearer, and also shows how the maximum load varies for a given length and other properties.
Next on the list is the amount of sideways force present in conjunction with the end force. If you were pushing on your ruler, but not so hard as to make it buckle, and then also pushed it sideways, that would induce buckling at a much lower level of compressive force. For example, the boom of a loose footed mainsail is under pure compression so long as the clew and mainsheet are more or less in the same place. It is not too great an idea to convert to a centre mainsheet, since that will induce bending somewhere around the middle of the spar, and you may find it bending alarmingly, even breaking. Similarly, lacing the sail to the boom may have the same effect. It is however possible that doing both will cancel out! In a similar fashion, you should avoid introducing bending in your bowsprit, as I mentioned in an earlier article. Finally, buckling depends on the shape of the section, or rather the sectional moment of inertia. For example for a given amount of material, a tube has higher inertia than a solid bar.
So buckling performance doesn’t have much to do with the strength of the base material. All other things being equal, a piece of mild steel will buckle at the same time as a piece of stainless steel, and also at the same time as a piece of high tensile steel. Finally getting back to our mast, we now find the diameter needs to go up to 100mm for a keel stepped mast, and 110mm diameter for a deck stepped one. That is still a pretty useful saving of weight, cost and windage over the original 280mm.
So far so good, but now we have to sort out the stay(s). The example I’m using here has a mast of 6m and a beam of 2m, so that gives me a staying angle of 9.5o or so. That is about the minimum feasible, though this rule has often to be stretched a tad when considering bowsprits. Anyway, the 500kg load is inducing about 3 tonnes in the stay. Since that is in tension we can use the full strength of the material, and that equates to about a 6mm wire, a 16mm modern rope and about a 40mm natural rope, or 4 x 20mm ropes. You can see why, in the days when rope was made from the same stuff as the masts – basic plant material – there were a good many stays in use. You can also see why it was (and is) worth trying to widen the shroud base by the use of channels. In our example, a local increase in beam of 0.2m reduces the loads in both the mast and the stays to about 2.5 tonnes, allowing a further reduction of mast size to 90 or 100mm, and stays to 5mm wire, 14mm modern rope and 36mm natural rope, or 3 x 20mm ropes. Again, useful savings.
Spreading the load
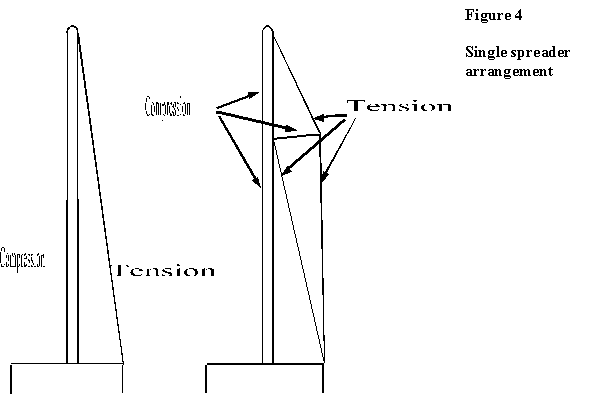
For even more prizes, you fit a set of spreaders – Figure 4. Doing so has three real benefits. The first is that the shroud angle is increased, so decreasing the shroud tension and the topmast compression. Secondly, the mast is split into “panels”, i.e. their effective length is reduced, so increasing the buckling load for a given section. Lastly, and this is a touch esoteric, splitting the panels also forces a particular shape that the mast will fail in under buckling. In effect the fixity of the end at the spreader is somewhere between pinned and fixed because there must be a continuous curve joining the mast below the spreader to the mast above it. In practice, though, one usually makes the assumption that both the upper and lower parts of the mast are pinned at this point.
The drawback with spreaders is that they introduce a sideways force in the middle of the mast. To overcome that, lower shrouds are fitted (except in racing dinghies and similar craft where spreaders are used deliberately to influence the mast bend ). To the sample mast I’ve added a set of spreaders two thirds of the way up the mast, and made them 90% of the width of the beam. The shroud angles have gone up to 24o (caps) and 14o (lowers), well above the minimum of 9o. Shroud tensions are now 1.24 tonnes – 4mm wire – for the caps and 1.93 tonnes – 5mm wire – for the lowers. Though the lower part of the mast is still subject to about 3 tonnes compression, the topmast compression is down to 1.13 tonnes. This allows a 50mm topmast, and 75 or 90mm lower mast diameters, depending on deck or keel stepping. The spreaders themselves take a load of about 0.5 tonne, and because they too can be considered as slender, need a section of about 45mm x 20mm if made of the same stuff as the mast.
So we have here the beginnings of a progressive trade-off involving weight, windage, complexity and cost which can be carried to the umpteenth degree by adding more and more sets of spreaders. For us ordinary mortals, two sets is usually about the limit for sails which run in tracks on the mast, and one set is sometimes possible for sails whose attachment to the mast involve lacing, hoops, jaws or saddles.
That, I hope, is a few basic principles sorted out, using a “model” which has been merely a device for illustrating a set of ideas, but which has little or no relationship to real life boats. In the next article, I’ll move a bit further toward reality by looking at design loads and some better assumptions on sail loads.